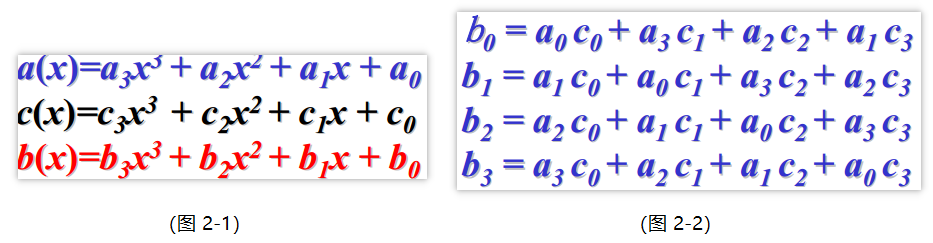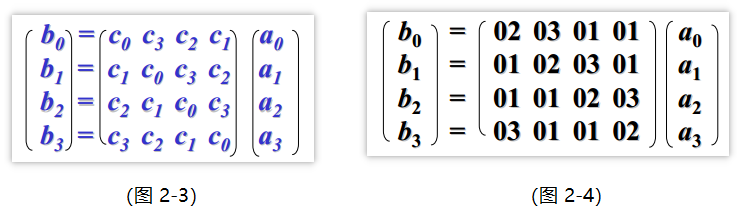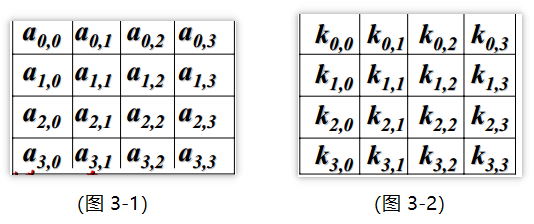AES 加密算法实现
上次实现了 DES 加密算法,接下来继续深入同为对称加密算法并广为应用的 AES 算法。
一. 概述
美国政府在1997年9月12日公开征集更高效更安全的替代DES加密算法,第一轮共有15种算法入选,其中5种算法入围了决赛,分别是MARS,RC6,Rijndael,Serpent和Twofish。又经过3年的验证、评测及公众讨论之后Rijndael算法最终入选。
Rijndael算法之所以最终能够被选为AES的原因是其安全、性能好、效率高、实用灵活。
Rijndael算法支持多种分组及密钥长度,介于128-256之间所有32的倍数均可,最小支持128位,最大256位,而AES标准支持的分组大小固定为128位,密钥长度有3种选择:128位、192位及256位。
二. AES算法的数学基础
Rijndaels算法中的许多运算是按字节和4字节的字来定义的。把一个字节看成是在有限域GF(2^8)上的一个元素。有限域(Finite Field)又名伽罗瓦域(Galois field),简单言之就是一个满足特定规则的集合,集合中的元素可以进行加减乘除运算,且运算结果也是属于此集合。
1. 有限域
AES的基础域是有限域 GF(2⁸)
- 一个字节的全体256种取值构成一个GF(2⁸)
- 一个GF(2)上的8次既约多项式可生成一个 GF(2⁸)
- GF(2⁸)的全体元素构成加法交换群、线性空间。
- GF(2⁸)的非零元素构成乘法循环群。
2. AES在有限域上的表示
有限域GF(2⁸)上的元素有多种表示方法,为了方便,Rijndaels算法采用多项式表示法,下面是与还表示方法相关的几个定义
定义1 : 一个由比特位b₇b₆b₅b₄b₃b₂b₁b₀ 组成的字节可表示成系数为(0, 1)的二进制多项式:b₇X⁷ + b₆X⁶ + b₅X⁵ + b₄X⁴ + b₃X³ + b₂X² + b₁X + b₀
例:字节57=01010111的多项式表示为: $$x^6 + x^4 + x^2 + x + 1$$
定义2 : 在GF(2⁸)上的加法定义为二进制多项式的加法,其系数按位模2加。
例: 57+83=D4等价于 $$(x^6+x^4+x^2+x+1)⊕(x^7+x+1)= x^7+x^6+x^4+x^2$$
定义3 : 在GF(2⁸)上的乘法定义为二进制多项式的乘积模一个次数为8的不可约多项式 $$m(x) = x^8+x^4+x^3+x+1$$
其系数的十六进制表示为11B
例: 57×83=C1等价于
$$(x^6+x^4+x^2+x+1)×(x^7+x+1) \ mod \ m (x) = x^{13 }+ x^{11}+x^9+x^8+x^6+x^5+x^4+x^3+1 \ mod \ x^8+x^4+x^3+x+1 = x^7+x^6+1 $$
定义4 : 在GF(2⁸)中,二进制多项式b(x)满足乘法逆为式a(x)b(x) mod m(x) = 1的二进制多项式。
定义5 : 在GF(2⁸)中,倍乘函数xtime(b(x))定义为x·b(x) mod m(x)。具体的运算规则是:把字节B左移一位,若b₇=1, 则减去m(x),而在GF(2⁸)上加减法等价,即加上m(x)
例:$$xtime(57)=x(x^6+x^4+x^2+x+1)= x^7+x^5+x^3+x^2+x $$
$$xtime(83)=x(x^7+x+1)= x^8+x^7+x \ mod \ m(x) = x^7+x^4+x^3+1 \ mod \ m(x) $$
3. AES的字表示与运算
3.1. 字表示
AES数据处理的单位是字节和字,一个字由四个字节组成,表示为系数取自GF(2⁸)上的次数低于4次的多项式
例: 字57 83 4A D1等价于 $$57x^3+83x^2+4Ax+D1$$
3.2. 字运算
字运算是基于上述关于AES在GF(2⁸)中的运算规则的。
字加法 : 两多项式系数按位模2加
字乘法 : 设a和c是两个字, a(x)和c(x)是其字多项式, AES定义a和c的乘积b为 $$b(x)=a(x)c(x) \ mod \ x^4+1$$
如:设a(x)、c(x)和b(x)分别分别如下面(图 2-1)中所示,由b(x) = a(x)c(x) mod x⁴+1得(图 2-1)表达式组
写成矩阵形式如下面的(图 2-3)所示,x⁴+1是可约多项式,字c(x)不一定有逆,但AES选择的c(x)有逆, $$c(x) =03x^3+01x^2+01x+02$$
从而使得b(x)的表达式可以使用上面(图 2-4)的矩阵表示,从而使得下面的MixColumns变换变为矩阵的乘法运算。
字x乘法 : $$p(x)=xb(x) \ mod \ x^4+1$$ 矩阵形式如下图所示,因为模x⁴+1,字x乘法相当于按字节循环移位
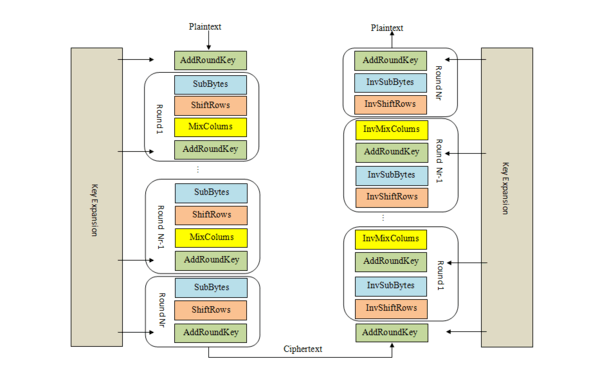
三. AES的加密过程
1. 状态
在AES中除了字节和字外,还有一种被称为状态的数据处理方式,它用来存储加解密过程中的中间数据,一般用以字节为元素的矩阵或二维数组表示。
如果用Nb代表明密文所含的字数。 Nk代表密钥所含的字数。 Nr代表迭代轮数,则当Nb和Nk都等于4时的状态与密钥数组分别如下面的(图 3-1)和(图 3-2)所示
根据Rijndael算法的定义,加密轮数会针对不同的分组及不同的密钥长度选择不同的数值
2. 加密过程概述
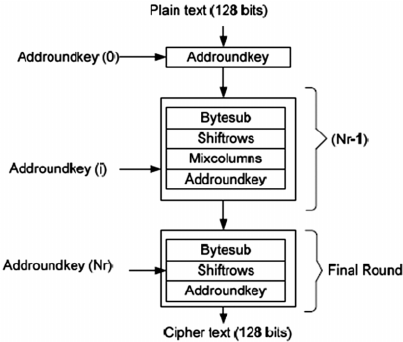
AES加密算法的主要步骤有
- 轮密钥生成
- 初始轮密钥加变换:将最初的第一个(Nk个字长)轮密钥亦即主密钥与初始状态进行比特位异或操作
- 标准轮(前9, 11 或 13轮)变换:
- S盒变换
- 行移位变换
- 列混合变换
- 轮密钥加变换
- 最后一轮(第10, 12或14轮)变换
- S盒变换
- 行移位变换
- 轮密钥加变换
3. AES有限域上的加法
|
|
4. 轮密钥生成
轮密钥根据密钥产生算法通过主密钥得到。密钥产生分两步进行:密钥扩展和轮密钥选择,且郡守以下规则
- 轮密钥的比特总数为明文数据块长度与轮数加1的积。例如,对于128位的分组长度和10轮迭代,轮密钥长度为128 x (10 + 1) = 1408位,即11个状态长
- 首先将用户密钥扩展为一个扩展密钥
- 再从扩展密钥中选出轮密钥:第一个轮密钥由扩展中的前Nb个字组成(即原主密钥),第二个轮密钥是接下来的Nb个字,以此类推。
4.1. 密钥扩展
用一个字元素的一维数组W[Nb*(Nr+1)]表示扩展密钥。把密钥放在该数组最开始的Nk个字中,其它的字由它前面的字经过处理后得到。分Nk≤6 和Nk>6两种密钥扩展算法:
① Nk≤6的密钥扩展
- 最前面的Nk个字是由主密钥填充
- 之后的每一个字W[j]等于前面的字W[j-1]与Nk个位置之前的字W[j-Nk]的异或
- 而且对于Nk的整数倍的位置处的字,在异或之前,对W[j-1]进行Rotl变换和ByteSub变换,再异或一个轮常数Rcon 。
Rotl是一个字里的字节循环左移函数, 设 W =(A, B, C, D) , 则Rotl(W) = (B, C, D, A)。 轮常数Rcon与Nk无关,且定义为:
- Rcon[i] = (RC [i],‘00’, ‘00’, ‘00’),
- RC[0] = ‘01’,
- RC[i] = xtime(RC[i-1])
② Nk>6 的密钥扩展 与Nk≤6 的密钥扩展相比, Nk>6 的密钥扩展的不同之处在于:如果j被Nk除的余数=4,则在异或之前,对W[j-1]进行ByteSub变换。
增加ByteSub变换,是因为当Nk>6时密钥很长,仅仅对Nk的整数倍的位置处的字进行ByteSub变换,就显得ByteSub变换的密度较稀,安全程度不够强。
4.2. 轮密钥的选择
根据分组的大小,依次从扩展密钥中取出轮密钥。前面的Nb个字作为轮密钥0,接下来的Nb个字作为轮密钥1,以此类推
4.3. 代码实现
|
|
5. AES基本变换
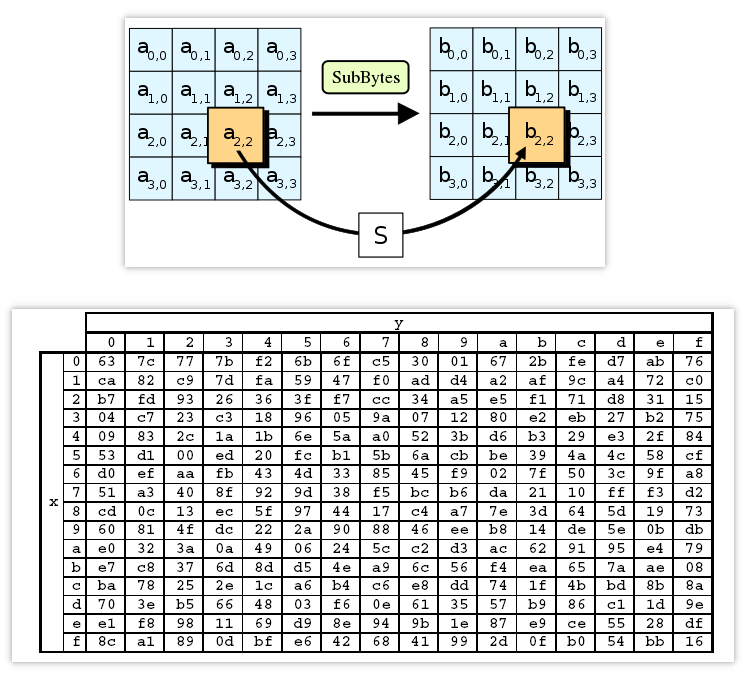
5.1. S盒变换
一种作用在状态中每一个字节上的非线性变换,对比于DES
- 因为AES-126明文数据块为16个字节,所以AES使用16个相同的S盒(其实是可重复16次使用同一个);DES使用8个不相同的S盒。
- AES的S盒有8位输入8位输出,是一种非线性置换;DES的S盒有6位输入4位输出,是一种非线性压缩。
AES的S盒变换可按以下两步进行:
- 将输入字节用其GF(2⁸)上的逆来代替
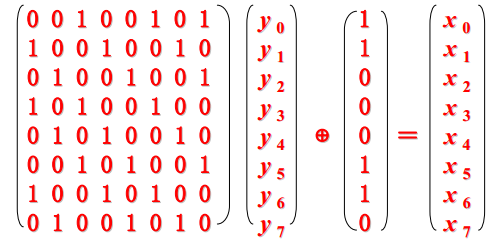
- 对上面的结果作如下的仿射变换:(以x₀- x₇作输入,以y₀- y₇作输出)
需要注意的是:
- S盒变换的第一步是把字节的值用它的乘法逆来代替,是一种非线性变换。
- 第二步是仿射运算,是线性变换。
- 由于系数矩阵中每列都含有5个1,这说明改变输入中的任意一位,将影响输出中的5位发生变化。
- 由于系数矩阵中每行都含有5个1,这说明输出中的每一位,都与输入中的5位相关。
代码实现
通过建表查表代替运算,同时将该操作拆分为substituteState、substituteWord和substituteByte三个子操作
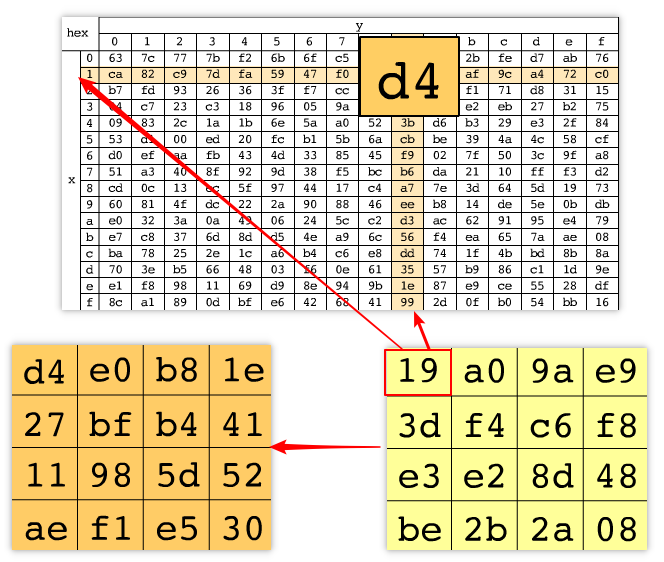
实现S盒最快的方法就是,直接算出S盒的变换结果并造表存储,使用时直接查表(表大小为256个字节)。查表的方法是:取一个字节的高低4位分别作为行号和列号,通过行列号定位到的表中的元素即为新的替代字节。如下图左表中的d4,
|
|
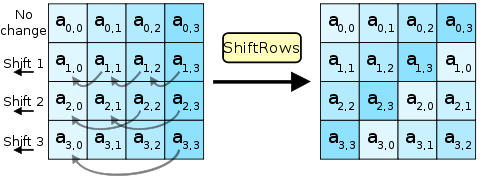
5.2. 行移位变换
行移位变换对状态的行进行循环移位。第0行不移位,第1行移C₁字节,第2行移C₂字节,第3行移C₃字节。C₁,C₂,C₃按表取值:
| Nb | C1 | C2 | C3 |
|---|---|---|---|
| 4 | 1 | 2 | 3 |
| 6 | 1 | 2 | 3 |
| 8 | 1 | 2 | 3 |
行移位变换属于置换,属于线性变换,本质在于把数据打乱、重排,起扩散作用。
代码实现
|
|
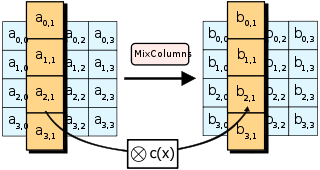
5.3. 列混合变换
列混合变换把状态的列视为GF(2⁸)上的多项式a(x),乘以一个固定的多项式c(x),并模x⁴+1: $$b(x)=a(x)c(x) \ mod \ x^4+1, c(x)=03x^3+01x^2+01x+02$$
需要注意的是:
- 列混合变换属于线性变换,起扩散作用。
- c(x)与x⁴ + 1互素,从而保证c(x)存在逆多项式d(x),而 c(x)d(x) = 1 mod x⁴ + 1 。只有逆多项式d(x)存在,才能正确进行解密
代码实现
|
|
6. 对外加密接口
- 将字符串形式的明文和密钥分别转换为N_b个字长的状态和N_k个字长的主密钥数组
- 通过主密钥数组生成轮密钥数组
- 将二维轮密钥数组转换成三维数组方便以N_k个字长为单位获取轮密钥
- 调用coreEncrypt方法,指定S盒运算表,列混合中用到的CX运算表和行变换每个字节的移位规则表
- 将最后获取到密文状态用Base64编码
|
|
7. 核心加密逻辑
|
|
四. 解密过程
说到加密先纵观整个AES的加解密流程,由于Rijndael算法不是对合运算,所以其解密算法与加密算法不同,根据解密算法应当是加密算法的逆,最直接的做法就是把加密算法倒序执行,便得到解密算法,但是这样不便于工程实现。
由于Rijndael算法的巧妙设计,使得我们只需稍微改变密钥扩展策略,同时把加密算法的基本运变换成逆变换,便得到解密算法,其算法结构其实与加密算法的结构相同。
1. AES基本逆变换
1.1. AddRoundKey
轮密钥加变换的逆就是其本身,即 $$ (AddRoundKey)^{-1}= AddRoundKey $$
1.2. ShiftRows
行移位变换的逆是状态的后三行分别移位N_b - C₁, N_b - C₂, N_b - C₃个字节。
1.3. MixColumns
因为列混合变换是把状态的每一列都乘以一个固定的多项式c(x): $$b(x)=a(x)c(x) \ mod \ x^4+1 $$ 所以列混合变换的逆就是状态的每列都乘以c(x)的逆多项式d(x): $$d(x)=(c(x) )^{-1} \ mod \ x^4+1 ,c(x)=03x^3+01x^2+01x+02,d(x)=0Bx^3+0Dx^2+09x+0E $$
1.4. SubBytes
S盒变换的逆要先进行逆仿射变换,再把每个字节用其在GF(2⁸)中的逆来代替。
1.5. KeyExpansion
解密的密钥扩展与加密的密钥扩展不同,其定义如下:
- 使用加密算法的密钥扩展
- 把InvMixColumn应用到除第一和最后一轮外的所有轮密钥上
另外得到的逆轮密钥数组在轮变换中需要倒序使用,即Round₁使用roundKey_(Nr+1)
2. 对外的解密接口
- 使用Base64编码将密文解码并得到初始状态,获取密钥数组
- 调用私有的核心解密函数得到解密后的明文状态
- 将明文状态还原为字符串(不考虑中文编码)
|
|
3. 核心解密逻辑
获取加密轮密钥逆变换数组,复用核心加密函数即可,主要差别在于逆变换,大体步骤如下
- 使用加密算法的密钥扩展得到轮密钥数组,并对之进行维数处理
- 对中间N_r-1个密钥进行逆列混合变换
- 为了便于操作将上述步骤得到的解密轮密钥数组逆转,这样便可通过改变参数复用加密算法的结构
|
|
五. 测试
|
|
1. 加密结果
##################### encryption #####################
plaintext text passwordTextCase
key text simpleKeyCase123
initial plaintext state 70617373776f72645465787443617365
initial key state 73696d706c654b657943617365313233
RoundKeys
[RoundKey 1] 73696d706c654b657943617365313233
[RoundKey 2] b54aae3dd92fe558a06c842bc55db618
[RoundKey 3] fb04039b222be6c3824762e8471ad4f0
[RoundKey 4] 5d4c8f3b7f6769f8fd200b10ba3adfe0
[RoundKey 5] d5d26ecfaab5073757950c27edafd3c7
[RoundKey 6] bcb4a89a1601afad4194a38aac3b704d
[RoundKey 7] 7ee54b0b68e4e4a62970472c854b3761
[RoundKey 8] 8d7fa49ce59b403acceb071649a03077
[RoundKey 9] ed7b51a708e0119dc40b168b8dab26fc
[RoundKey 10] 948ce1fa9c6cf0675867e6ecd5ccc010
[RoundKey 11] e9362bf9755adb9e2d3d3d72f8f1fd62
N = 1
SubBytes 7b30727baf67127cd8f7d4c5f75383b1
ShiftRows 7b67d4b1aff7837bd853727cf73012c5
MixColumns 3a636747bfbfc8685094ebaa7264b7b1
RoundKey b54aae3dd92fe558a06c842bc55db618
AddRoundKeys 8f29c97a66902d30f0f86f81b73901a9
N = 2
SubBytes 73a5ddda3360d8048c41a80ca9127cd3
ShiftRows 7360a8d333417cda8c12dd04a9a5d80c
MixColumns 3d8336e003efffc7ecd033486987b385
RoundKey fb04039b222be6c3824762e8471ad4f0
AddRoundKeys c687357b21c419046e9751a02e9d6775
N = 3
SubBytes b4179621fd1cd4f29f88d1e0315e859d
ShiftRows b41cd19dfd8885219f5e96f23117d4e0
MixColumns 1b79ad2bc6430753a370fb8d6f98ae4b
RoundKey 5d4c8f3b7f6769f8fd200b10ba3adfe0
AddRoundKeys 46352210b9246eab5e50f09dd5a271ab
N = 4
SubBytes 5a9693ca56369f6258538c5e033aa362
ShiftRows 5a368c625653a3ca583a936203969f5e
MixColumns 00dbc99030c41d850fe0f98566d052b0
RoundKey d5d26ecfaab5073757950c27edafd3c7
AddRoundKeys d509a75f9a711ab25875f5a28b7f8177
N = 5
SubBytes 03015ccfb8a3a2376a9de63a3dd20cf5
ShiftRows 03a3e6f5b89d0ccf6ad25c373d01a23a
MixColumns eb9a73b1144277c7d206595ee1f82d90
RoundKey bcb4a89a1601afad4194a38aac3b704d
AddRoundKeys 572edb2b0243d86a9392fad44dc35ddd
N = 6
SubBytes 5b31b9f1771a6102dc4f2d48e32e4cc1
ShiftRows 5b1a2dc1774f4cf1dc2eb902e3316148
MixColumns 74d9434382cca8636a529deca76ac8fe
RoundKey 7ee54b0b68e4e4a62970472c854b3761
AddRoundKeys 0a3c0848ea284cc54322dac02221ff9f
N = 7
SubBytes 67eb3052873429a61a9357ba93fd16db
ShiftRows 673457db879316521afd30a693eb29ba
MixColumns 1e2d8b67ffd2ceb3be0d76b4889fff03
RoundKey 8d7fa49ce59b403acceb071649a03077
AddRoundKeys 93522ffb1a498e8972e671a2c13fcf74
N = 8
SubBytes dc00150fa23b19a7408ea33a78758a92
ShiftRows dc3ba392a28e8a0f407515a77800193a
MixColumns dfc617d8532f32e7ad32edf5d36904e5
RoundKey ed7b51a708e0119dc40b168b8dab26fc
AddRoundKeys 32bd467f5bcf237a6939fb7e5ec22219
N = 9
SubBytes 237a5ad2398a26daf9120ff3582593d4
ShiftRows 238a0fd4391293d2f9255ada587a26f3
MixColumns 18e9d05305617b7506871dc0eb356049
RoundKey 948ce1fa9c6cf0675867e6ecd5ccc010
AddRoundKeys 8c6531a9990d8b125ee0fb2c3ef9a059
N = 10
SubBytes 644dc7d3eed73dc958e10f71b299e0cb
ShiftRows 64d70fcbeee1e0d35899c7c9b24d3d71
RoundKey e9362bf9755adb9e2d3d3d72f8f1fd62
AddRoundKeys 8de124329bbb3b4d75a4fabb4abcc013
encrypted text jeEkMpu7O011pPq7SrzAEw==
2. 解密结果
##################### decryption #####################
encrypted text jeEkMpu7O011pPq7SrzAEw==
key text simpleKeyCase123
initial encrypted state 8de124329bbb3b4d75a4fabb4abcc013
initial key state 73696d706c654b657943617365313233
RoundKeys
[RoundKey 1] 73696d706c654b657943617365313233
[RoundKey 2] b54aae3dd92fe558a06c842bc55db618
[RoundKey 3] fb04039b222be6c3824762e8471ad4f0
[RoundKey 4] 5d4c8f3b7f6769f8fd200b10ba3adfe0
[RoundKey 5] d5d26ecfaab5073757950c27edafd3c7
[RoundKey 6] bcb4a89a1601afad4194a38aac3b704d
[RoundKey 7] 7ee54b0b68e4e4a62970472c854b3761
[RoundKey 8] 8d7fa49ce59b403acceb071649a03077
[RoundKey 9] ed7b51a708e0119dc40b168b8dab26fc
[RoundKey 10] 948ce1fa9c6cf0675867e6ecd5ccc010
[RoundKey 11] e9362bf9755adb9e2d3d3d72f8f1fd62
inverse roundKeys
[RoundKey 1] e9362bf9755adb9e2d3d3d72f8f1fd62
[RoundKey 2] 708e03febe111cd46ee2ba036852f407
[RoundKey 3] 513f2d23ce9f1f2ad0f3a6d706b04e04
[RoundKey 4] 16b3b0df9fa032091e6cb9fdd643e8d3
[RoundKey 5] de6e462d891382d681cc8bf4c82f512e
[RoundKey 6] 0dc56d9f577dc4fb08df092249e3dada
[RoundKey 7] e0240c6e5ab8a9645fa2cdd9413cd3f8
[RoundKey 8] e0ec63caba9ca50a051a64bd1e9e1e21
[RoundKey 9] a13297635a70c6c0bf86c1b71b847a9c
[RoundKey 10] 1d7fded0fb4251a3e5f60777a402bb2b
[RoundKey 11] 73696d706c654b657943617365313233
N = 1
SubBytes 8c0dfb5999e0a0a95ef931123e658b2c
ShiftRows 8c6531a9990d8b125ee0fb2c3ef9a059
MixColumns 53040c2a87038f0697c7e0d93028d2f4
RoundKey 708e03febe111cd46ee2ba036852f407
AddRoundKeys 238a0fd4391293d2f9255ada587a26f3
N = 2
SubBytes 32cffb195b39227f69c2467a5ebd237e
ShiftRows 32bd467f5bcf237a6939fb7e5ec22219
MixColumns 8d048eb16c1195259086b3707eb0573e
RoundKey 513f2d23ce9f1f2ad0f3a6d706b04e04
AddRoundKeys dc3ba392a28e8a0f407515a77800193a
N = 3
SubBytes 934971741ae6cffb723f2f89c1528ea2
ShiftRows 93522ffb1a498e8972e671a2c13fcf74
MixColumns 7187e7041833245b0491895b45a8c169
RoundKey 16b3b0df9fa032091e6cb9fdd643e8d3
AddRoundKeys 673457db879316521afd30a693eb29ba
N = 4
SubBytes 0a28da9fea22ff48432108c5223c4cc0
ShiftRows 0a3c0848ea284cc54322dac02221ff9f
MixColumns 85746becfe5cce275de232f62b1e3066
RoundKey de6e462d891382d681cc8bf4c82f512e
AddRoundKeys 5b1a2dc1774f4cf1dc2eb902e3316148
N = 5
SubBytes 5743fadd02925d2b93c3db6a4d2ed8d4
ShiftRows 572edb2b0243d86a9392fad44dc35ddd
MixColumns 0e668b6aefe0c834620d551574e278e0
RoundKey 0dc56d9f577dc4fb08df092249e3dada
AddRoundKeys 03a3e6f5b89d0ccf6ad25c373d01a23a
N = 6
SubBytes d571f5779a75815f587fa7b28b091aa2
ShiftRows d509a75f9a711ab25875f5a28b7f8177
MixColumns ba12800c0ceb0aae07985ebb42aa4ca6
RoundKey e0240c6e5ab8a9645fa2cdd9413cd3f8
AddRoundKeys 5a368c625653a3ca583a936203969f5e
N = 7
SubBytes 4624f0abb95071105ea222abd5356e9d
ShiftRows 46352210b9246eab5e50f09dd5a271ab
MixColumns 54f0b2574714202b9a44f24f2f89cac1
RoundKey e0ec63caba9ca50a051a64bd1e9e1e21
AddRoundKeys b41cd19dfd8885219f5e96f23117d4e0
N = 8
SubBytes c6c451752197677b6e9d35042e8719a0
ShiftRows c687357b21c419046e9751a02e9d6775
MixColumns d2523fb06931ba1a33941cb3b221a290
RoundKey a13297635a70c6c0bf86c1b71b847a9c
AddRoundKeys 7360a8d333417cda8c12dd04a9a5d80c
N = 9
SubBytes 8f906fa966f8017af039c930b7292d81
ShiftRows 8f29c97a66902d30f0f86f81b73901a9
MixColumns 66180a6154b5d2d83da5750b5332a9ee
RoundKey 1d7fded0fb4251a3e5f60777a402bb2b
AddRoundKeys 7b67d4b1aff7837bd853727cf73012c5
N = 10
SubBytes 030a19561b2641032d501e0126083907
ShiftRows 03081e031b0a39012d26190726504156
RoundKey 73696d706c654b657943617365313233
AddRoundKeys 70617373776f72645465787443617365
plaintext passwordTextCase
六. 说明
1. 源码
本AES实现的代码已经发布到Github,如果你觉得写得还不错,欢迎star和fork; 如果对代码有疑惑,欢迎通过邮箱linfengit@qq.com与我讨论
2. TODO
- 本例子以AES-128为例,明文小于128位应该进行填充; 大于128位应该进行分组,待加密完成后进行密文的合并
- 没有就数据编码进行扩展,暂不支持中文数据加密
- 实现的是最简单的电码本(ECB)工作模式,暂不支持其他模式明文数据模式
七. 参考
- FIPS 197 – Advanced Encryption Standard
- 动画演示AES运行过程
- 《密码学引论》(第三版,张焕国、唐明编著,武汉大学出版社)